Redes Neurais Artificiais

Introdução

Imagine que você está tentando ensinar um computador a reconhecer gatos em fotos. Como você explicaria para uma máquina o que torna um gato um gato? As orelhas pontudas? Os bigodes? O formato dos olhos? Essa é exatamente a inspiração por trás das Redes Neurais Artificiais (RNA) — modelos computacionais que tentam imitar como nosso cérebro processa informações complexas.

As RNAs são uma das família de arquiteturas de modelos para aprendizado de máquina, especialmente úteis quando:

• Precisamos capturar padrões não lineares complexos que modelos tradicionais não conseguem
• Temos grandes volumes de dados e queremos que o próprio modelo descubra as características importantes
• Queremos processar diferentes tipos de informação como imagens, texto, áudio ou séries temporais
• O problema é complexo demais para ser resolvido com regras simples

Quando usar Redes Neurais?

Considere RNAs quando: - Os dados mostram relações claramente não lineares entre entradas e saídas - Você tem muitos dados e alta dimensionalidade - Precisa de extração automática de características (o modelo descobre sozinho o que é importante) - Quer processar múltiplas modalidades (imagem + texto, por exemplo)

Talvez outras técnicas sejam melhores se: - Você tem poucos dados ou o problema é simples — experimente modelos lineares, árvores de decisão ou kNN primeiro - Precisa de interpretabilidade total — prefira modelos mais transparentes como árvores ou regressão linear - Tem pressa para colocar em produção — RNAs precisam de mais tempo para ajuste fino

Quando as redes neurais são especialmente recomendadas?

Apenas para problemas simples com poucos dados

Somente quando precisamos de máxima interpretabilidade

Para problemas com padrões não lineares complexos e grandes volumes de dados

Exclusivamente para processamento de texto

Submit

Redes neurais são boas em cenários com relações complexas não lineares, grandes datasets e quando precisamos que o modelo aprenda automaticamente quais características são importantes.

Intuição RNA

Para conhecer um pouco da historia, vale a pena assistir esse vídeo.

O neurônio biológico

Nosso cérebro possui cerca de 86 bilhões de neurônios interconectados. Cada neurônio é como uma pequena unidade de processamento que:

Dendritos → Soma → Axônio → Sinapses
    ↑        ↑       ↑        ↑
  Entrada  Processamento  Transmissão  Saída

Como funciona a comunicação neural:

1. Dendritos recebem sinais químicos de outros neurônios
2. Soma (corpo celular) soma e processa todos esses sinais
3. Se a soma ultrapassa um limiar, o neurônio "dispara"
4. O sinal elétrico percorre o axônio
5. Sinapses liberam neurotransmissores para outros neurônios

É como uma corrente de dominós inteligentes — cada peça decide se vai derrubar a próxima baseado na força do impulso que recebeu!

Qual é a função principal do soma (corpo celular) no neurônio biológico?

Receber sinais de outros neurônios

Transmitir sinais para outros neurônios

Integrar e processar os sinais recebidos

Armazenar memórias de longo prazo

Submit

O soma é responsável por integrar (somar) todos os sinais recebidos pelos dendritos e decidir se o neurônio deve "disparar" ou não, baseado em um limiar de ativação.

O neurônio artificial

Como transformamos neurônios em números

Pegamos a ideia do neurônio biológico e criamos uma versão matemática simplificada. Imaginem o neurônio artificial como uma calculadora especializada que:

x₁ ──w₁──┐
x₂ ──w₂──┤
    ...  ├─→ Σ ──→ f(net) ──→ y
xₙ ──wₙ──┘
    b ───┘

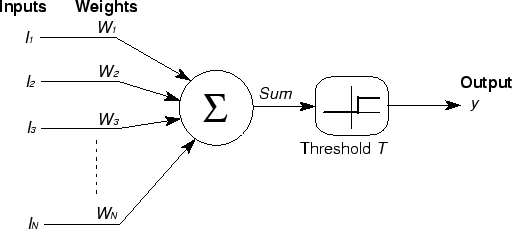
O que acontece aqui:

1. Entradas (x₁, x₂, ..., xₙ): Os "dendritos" — informações que chegam
2. Pesos (w₁, w₂, ..., wₙ): A "força das sinapses" — o quanto cada entrada importa
3. Bias (b): O "limiar de ativação" — um ajuste fino
4. Soma ponderada: Multiplicamos cada entrada pelo seu peso e somamos tudo
5. Função de ativação (f): Decide se o neurônio "dispara" ou não

As equações fundamentais:

net = w₁×x₁ + w₂×x₂ + ... + wₙ×xₙ + b
y = f(net)

O que representam os "pesos" em um neurônio artificial?

O número de entradas do neurônio

A importância relativa de cada entrada na decisão final

O tipo de função de ativação utilizada

O valor mínimo para ativação do neurônio

Submit

Os pesos determinam o quanto cada entrada influencia na saída final do neurônio. Pesos maiores significam maior importância, enquanto pesos próximos de zero indicam que aquela entrada é quase irrelevante.

Funções de ativação

As funções de ativação são responsáveis por introduzir não-linearidades no modelo. Sem elas, a rede seria essencialmente um modelo linear e incapaz de aprender e representar dados complexos que requerem não-linearidade para sua modelagem.

A função de ativação é como o interruptor que decide se o neurônio vai "ligar" (disparar) ou "desligar". Cada tipo tem sua personalidade:

1. Função Degrau (Step)

f(x) = { 1, se x ≥ 0
       { 0, se x < 0

- Quando usar: Problemas simples de sim/não - Característica: Tudo ou nada, sem meio termo

2. Função Sigmóide

f(x) = 1 / (1 + e^(-x))

- Faixa: Entre 0 e 1 (ótimo para probabilidades!) - Vantagem: Suave e diferenciável - Problema: Pode "saturar" com valores muito grandes

3. Tangente Hiperbólica (tanh)

f(x) = (e^x - e^(-x)) / (e^x + e^(-x))

- Faixa: Entre -1 e 1 - Vantagem: Centrada no zero (melhor que sigmóide)

4. ReLU

f(x) = max(0, x)

• Regra: Se positivo, passa; se negativo, zero
• Por que é popular: Simples, rápida e resolve problemas de gradientes em redes profundas

Por que a função ReLU é tão popular em redes neurais modernas?

Porque sempre retorna valores entre 0 e 1

Porque é a mais complexa matematicamente

Porque é simples, rápida e resolve problemas de gradientes em redes profundas

Porque funciona melhor com dados negativos

Submit

ReLU (Rectified Linear Unit) se tornou popular porque sua simplicidade (max(0,x)) a torna computacionalmente eficiente e ajuda a resolver o problema do desvanecimento de gradientes em redes profundas.

Perceptron:

A história que mudou tudo

Em 1957, Frank Rosenblatt criou algo revolucionário: o Perceptron. Foi a primeira vez que uma máquina conseguiu "aprender" a separar coisas de forma automática. Imagine ensinar um computador a distinguir entre dois grupos de pontos apenas mostrando exemplos!

O Perceptron é como um neurônio artificial muito determinado — ele fica ajustando seus pesos até conseguir separar corretamente os dados. É o avô de todas as redes neurais modernas!

Como o Perceptron aprende

Entrada → Pesos → Soma → Ativação → Saída
x₁,x₂,...,xₙ → w₁,w₂,...,wₙ → Σ → f → y

O algoritmo de aprendizado (versão simplificada):

1. Inicializar: Comece com pesos aleatórios
2. Para cada exemplo de treino:
3. Calcule a saída: y = f(soma dos pesos × entradas)
4. Compare com a resposta correta
5. Se errou: Ajuste os pesos na direção certa
6. Se acertou: Continue para o próximo exemplo
7. Repita até parar de cometer erros

Qual foi a principal contribuição histórica do Perceptron?

Foi a primeira rede neural a processar imagens

Foi o primeiro algoritmo de aprendizado para redes neurais com garantia de convergência

Inventou as funções de ativação modernas

Criou o conceito de backpropagation

Submit

O Perceptron foi revolucionário porque demonstrou pela primeira vez que uma máquina podia aprender automaticamente a classificar dados, estabelecendo as bases para toda a área de redes neurais.

O Teorema da Convergência

A promessa do Perceptron: Se seus dados puderem ser separados por uma linha reta (ou hiperplano), o Perceptron sempre vai encontrar essa linha, em um número finito de passos. É como ter a garantia de que, se existe uma solução, você vai encontrá-la!

Objetivo deste exercício

Você poderá:

1. Ajustar manualmente os pesos $w_1, w_2$ e o viés $b$ para separar os pontos de cada classe.
2. Treinar automaticamente usando a regra de aprendizado do Perceptron.
3. Visualizar a fronteira de decisão mudando de posição conforme os parâmetros.

Atividade inicial:

• Escolha o problema AND e tente ajustar manualmente até atingir 100% de acurácia.
• Depois, avalie para problema da OR e observe o que acontece.
• Por fim, tente o problema XOR e observe o resultado.

Perceptron — Exercício Interativo

w₁: 0.00

w₂: 0.00

b: 0.00

Taxa (η lr): 0.10

Épocas: 30

Problema

AND OR XOR

Acurácia: —

mostrar grade

Treinar Reset

x₁, x₂ em [−0.2, 1.2] × [−0.2, 1.2] • azul = 0 • vermelho = 1 • linha preta = fronteira w₁x₁ + w₂x₂ + b = 0

Perguntas para reflexão

1. Por que o Perceptron consegue aprender AND mas não XOR?
2. O que acontece com a fronteira quando alteramos apenas o viés?
3. Como a taxa de aprendizado influencia a velocidade de convergência?

As limitações que mudaram a história

O Perceptron tinha um problema fatal: só funcionava para problemas linearmente separáveis.

O famoso problema XOR:

Entradas	Saída XOR
A B	Resultado
0 0	0
0 1	1
1 0	1
1 1	0

Não importa como você tente, não existe uma linha reta que separe corretamente os 1s dos 0s neste problema! Essa limitação quase matou a pesquisa em redes neurais nos anos 1970.

Por que o problema XOR foi tão significativo para a história das redes neurais?

Porque era muito complexo computacionalmente

Porque envolvia muitas variáveis de entrada

Porque demonstrou que o Perceptron não consegue resolver problemas não linearmente separáveis

Porque precisava de dados muito grandes para treinar

Submit

O XOR mostrou uma limitação fundamental do Perceptron: ele só funciona quando os dados podem ser separados por uma linha reta, o que levou ao "inverno da IA" até o desenvolvimento de redes com múltiplas camadas.

Multilayer Perceptron (MLP)

A solução para o problema XOR

Os cientistas descobriram algo incrível: se você empilhar neurônios em camadas, de repente consegue resolver problemas que pareciam impossíveis! O MLP (Multilayer Perceptron) nasceu dessa descoberta.

Como o MLP supera as limitações:

1. Camadas ocultas: Criam representações intermediárias dos dados
2. Múltiplas camadas: Cada camada aprende padrões mais complexos
3. Backpropagation: Um algoritmo inteligente que ensina todas as camadas simultaneamente

É como ter vários especialistas trabalhando em sequência — cada um pega o trabalho do anterior e o refina ainda mais!

A arquitetura em camadas

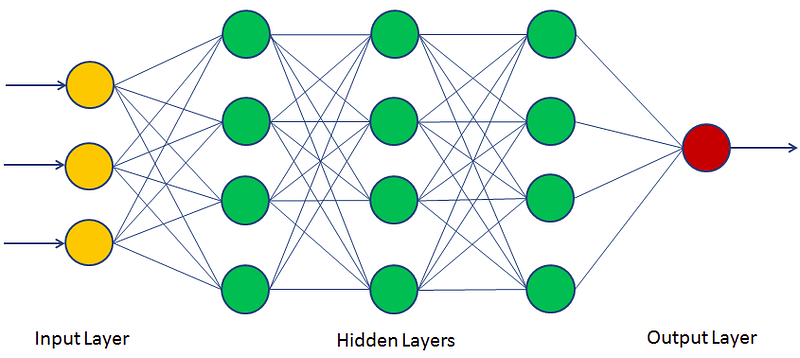
O que cada camada faz:

• Entrada: Recebe os dados originais
• Oculta(s): Transformam os dados em representações mais úteis
• Saída: Produz a resposta final

Objetivo deste exercício

Você deve:

1. Treinar um MLP para aprender o XOR usando backpropagation.
2. Alterar taxa de aprendizado, épocas e função de ativação (tanh/ReLU).
3. Visualizar a região de decisão sendo formada. Olhe a cor de fundo para saber a classe prevista para cada região. Use a linha preta apenas para ver onde a decisão muda (probabilidade ≈ 0.5).

Atividade inicial:

• Treine com tanh, η=0.10, 300 épocas.
• Verifique se a acurácia chega a 100%.
• Troque para ReLU e compare a convergência.

MLP 2–2–1 — XOR

Ativação

tanh ReLU

Taxa (η): 0.10

Épocas: 300

Batch

full (XOR completo) SGD (embaralha)

Acurácia: —

mostrar região de decisão

Treinar Reset

Pesos (ler/ajustar manualmente)

w11: w12: w21: w22: b1: b2: v1: v2: c:

x₁, x₂ em [−0.2, 1.2] × [−0.2, 1.2] • azul = 0 • vermelho = 1 • contorno preto ≈ p=0.5

Perguntas para reflexão

1. Por que o MLP consegue resolver o XOR, mas o Perceptron simples não?
2. Como a taxa de aprendizado afeta a convergência?

Qual é a principal vantagem das camadas ocultas em um MLP?

Reduzem o tempo de treinamento

Diminuem a quantidade de dados necessários

Permitem aprender representações não lineares dos dados

Simplificam a interpretação do modelo

Submit

As camadas ocultas permitem que a rede neural crie transformações não lineares dos dados de entrada, possibilitando resolver problemas como XOR que são impossíveis para um único neurônio.

Qual é a diferença fundamental entre um Perceptron e um MLP?

O Perceptron usa função ReLU, o MLP usa sigmóide

O Perceptron é mais rápido para treinar

O MLP possui camadas ocultas que permitem resolver problemas não lineares

O Perceptron funciona melhor com grandes datasets

Submit

A principal diferença é que o MLP possui camadas ocultas entre a entrada e saída, permitindo aprender padrões não lineares que o Perceptron (com apenas entrada e saída) não consegue capturar.

O Teorema da Aproximação Universal

Teorema incrível: Uma rede neural com apenas uma camada oculta e neurônios suficientes pode aproximar qualquer função contínua com a precisão que você quiser!

Em outras palavras: teoricamente, você pode ensinar uma rede neural a fazer qualquer coisa (desde que seja uma função matemática contínua). É como ter um "canivete suíço" matemático universal!

Atenção: o teorema não diz quantos neurônios você precisa — às vezes pode ser um número astronômico!

Guia prático: quantos neurônios usar?

Esta é uma das perguntas mais comuns: Quantos neurônios e quantas camadas devo colocar na minha rede?

Regras práticas históricas (use como ponto de partida, não como lei):

Para a camada oculta:

1. Regra dos ⅔:

neurônios ocultos ≈ (2/3 × neurônios de entrada) + neurônios de saída

2. Média geométrica:

neurônios ocultos ≈ √(entradas × saídas)

3. Experimentação incremental (recomendado hoje):

• Comece pequeno
• Monitore treino vs validação
• Aumente gradualmente
• Use regularização para evitar overfitting

Para o número de camadas:

• 1 camada oculta: Problemas que viram lineares após uma transformação
• 2 camadas: Qualquer função contínua (teorema da aproximação)
• 3+ camadas: Funções descontínuas e padrões muito complexos (Deep Learning!)

Segundo o Teorema da Aproximação Universal, quantas camadas ocultas são teoricamente necessárias para aproximar qualquer função contínua?

Infinitas camadas

Pelo menos 3 camadas

Apenas 1 camada oculta (com neurônios suficientes)

Depende do tipo de dados

Submit

O teorema estabelece que uma única camada oculta com neurônios suficientes pode aproximar qualquer função contínua, embora na prática múltiplas camadas muitas vezes sejam mais eficientes.