Backpropagation

Introdução

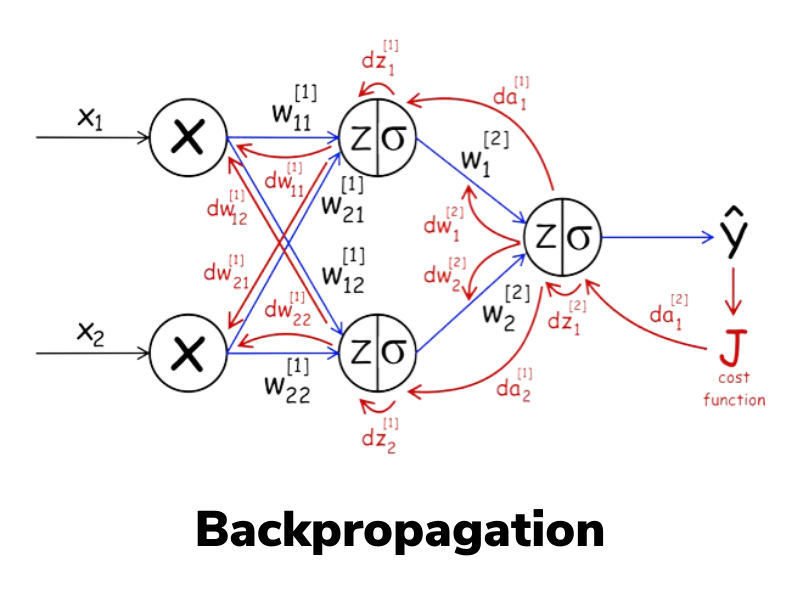
Sabemos que redes neurais são como calculadoras especializadas que podem resolver problemas complexos. Mas uma pergunta ficou no ar: como elas aprendem? Como uma rede neural descobre quais pesos usar para acertar as respostas?

Pense em ensinar um amigo a cobrar pênaltis. Não adianta dizer apenas “chute melhor”, isso é vago demais. É preciso dar instruções precisas, como: “mire um pouco mais para a esquerda”, “reduza a força do chute” ou “ajuste o ângulo do pé”.

O backpropagation faz exatamente isso, mas para redes neurais: é um método sistemático para indicar a cada neurônio o quanto e em que direção ajustar seus parâmetros, a fim de melhorar o resultado final.

Este algoritmo revolucionou a inteligência artificial e é a base de praticamente tudo que vemos hoje em IA, desde reconhecimento de voz até carros autônomos!

O problema do aprendizado

Encontrar os pesos para um perceptron é fácil porque há apenas um neurônio. Mas em uma rede com várias camadas, surge um problema: como saber qual neurônio da camada oculta é responsável pelo erro?

É como tentar descobrir qual jogador de um time de futebol errou quando o time perde — pode ter sido o goleiro, o zagueiro, o meio-campo ou o atacante. Todos contribuíram para o resultado final!

Por que o algoritmo de aprendizado do Perceptron não funciona diretamente em redes multicamadas?

Porque redes multicamadas são muito lentas

Porque usa muita memória computacional

Porque não sabemos como atribuir responsabilidade pelo erro aos neurônios das camadas ocultas

Porque as funções de ativação são diferentes

Submit

Em redes multicamadas, todos os neurônios contribuem para o resultado final, tornando difícil saber exatamente como ajustar cada peso individual quando há um erro na saída.

O Backpropagation

A solução é propagar o erro de volta através da rede, camada por camada. É como rastrear a origem de um problema:

1. Calcule o erro na saída (o quanto erramos)
2. Distribua a "culpa" para a última camada oculta
3. Continue distribuindo para as camadas anteriores
4. Ajuste os pesos baseado na "responsabilidade" de cada um

É como investigar um acidente: você começa pelo resultado e vai voltando para descobrir todas as causas que contribuíram.

Intuição Matemática

Função de Perda (Loss) e Entropia Cruzada Binária (BCE)

Em redes neurais, o treinamento envolve ajustar os parâmetros (pesos e biases) para que o modelo produza saídas o mais próximas possível das saídas desejadas. Para guiar esse ajuste, precisamos de uma métrica quantitativa que capture o quanto o modelo está errando. Essa métrica é a função de perda (ou função de custo, loss function), que mede a discrepância entre as predições do modelo ($\hat{y}$) e os rótulos verdadeiros ($y$).

Suponha uma tarefa de regressão linear, onde queremos prever um valor contínuo. Uma função de perda comum é o erro quadrático médio (Mean Squared Error, MSE):

• Para um único exemplo $i$:
  $$ \ell(\hat{y}^{(i)}, y^{(i)}) = \left( y^{(i)} - \hat{y}^{(i)} \right)^2 $$

• Para um lote (batch) de $m$ exemplos:
  $$ J = \frac{1}{m} \sum_{i=1}^{m} \ell\left( \hat{y}^{(i)}, y^{(i)} \right) = \frac{1}{m} \sum_{i=1}^{m} \left( y^{(i)} - \hat{y}^{(i)} \right)^2 $$

Aqui, o quadrado garante que erros positivos e negativos não se cancelem, e penaliza erros maiores de forma quadrática (ou seja, um erro de 2 é penalizado 4 vezes mais que um erro de 1, incentivando o modelo a evitar grandes desvios).

Requisitos para uma Boa Função de Perda

A função de perda deve ser diferenciável (quase em todos os pontos) para permitir o cálculo de gradientes via backpropagation. Além disso, ela deve ser convexa ou quasi-convexa em problemas ideais, facilitando a convergência para um mínimo global. O objetivo do treinamento é minimizar $J$ ajustando os pesos $\theta$ do modelo:
$$ \theta^* = \arg\min_{\theta} J(\theta) $$ Usamos otimização baseada em gradientes para isso, como o Gradiente Descendente.

Agora, foquemos em tarefas de classificação binária, onde $y \in \{0, 1\}$ (ex.: "é spam ou não?"). Aqui, a saída do modelo é tipicamente uma probabilidade $\hat{y} = \sigma(z) \in (0,1)$, onde $\sigma$ é a função Sigmoid aplicada ao logit $z$ (saída linear antes da ativação). A função de perda tipica é a Entropia Cruzada Binária (Binary Cross-Entropy, BCE) ou log loss:

$$\ell_{\text{BCE}}(y, \hat{y}) = -\left[ y \log(\hat{y}) + (1 - y) \log(1 - \hat{y}) \right]$$

• Interpretação Probabilística: A BCE deriva do negativo do logaritmo da verossimilhança (negative log-likelihood) sob uma distribuição de Bernoulli. Se $y=1$, a perda penaliza quando $\hat{y}$ está longe de 1 (ou seja, $\log(\hat{y})$ é muito negativo se $\hat{y}$ for pequeno). Se $y=0$, penaliza quando $\hat{y}$ está longe de 0. Isso incentiva predições "confiantes" apenas quando corretas; predições erradas e confiantes (ex.: $\hat{y}=0.99$ quando $y=0$) recebem penalidades altas devido ao logaritmo.

• Derivação Rápida do Gradiente: Uma propriedade chave da BCE combinada com Sigmoid é a simplificação do gradiente. Vamos derivar brevemente:
  A perda em termos do logit $z$ é $\ell(y, \sigma(z)) = -[y \log(\sigma(z)) + (1-y) \log(1 - \sigma(z))]$.
  Usando a regra da cadeia:
  $$ \frac{\partial \ell}{\partial z} = \frac{\partial \ell}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial z} = \left( \frac{\hat{y} - y}{\hat{y}(1 - \hat{y})} \right) \cdot \hat{y}(1 - \hat{y}) = \hat{y} - y $$ Essa simplificação torna o backpropagation computacionalmente eficiente e numericamente estável, evitando problemas como vanishing gradients em camadas profundas.

Para um batch:
$$ J_{\text{BCE}} = \frac{1}{m} \sum_{i=1}^{m} \ell_{\text{BCE}}(y^{(i)}, \hat{y}^{(i)}) $$

Extensão para Classificação Multiclasse

Para $K$ classes, use a ativação softmax na saída final ($\hat{y}_k = \frac{e^{z_k}}{\sum_{j=1}^K e^{z_j}}$) e a Entropia Cruzada Categórica:
$$ \ell_{\text{CE}}(y, \hat{y}) = -\sum_{k=1}^K y_k \log(\hat{y}_k) $$
onde $y$ é um vetor one-hot. O gradiente em relação aos logits também simplifica para $\frac{\partial \ell}{\partial z_k} = \hat{y}_k - y_k$, facilitando o treinamento.

Qual é o objetivo principal da função de custo no backpropagation?

Acelerar o treinamento da rede neural

Escolher a melhor arquitetura de rede

Medir quantitativamente o erro para guiar o ajuste dos pesos

Determinar o número ideal de neurônios

Submit

A função de custo quantifica o erro da rede, fornecendo uma métrica clara de quão distantes estamos do resultado desejado, permitindo ajustar os pesos na direção correta via gradientes.

O Gradiente: A Direção da Mudança

O gradiente de uma função $J(\theta)$ em relação aos parâmetros $\theta$ é um vetor que aponta na direção de maior aumento de $J$. Para minimizar $J$, movemos na direção oposta (descida). Matematicamente, para um parâmetro $\theta_j$:
$$ \frac{\partial J}{\partial \theta_j} $$
representa quanto $J$ muda se alterarmos $\theta_j$ infinitesimalmente.

Analogia da Montanha (com Toque Técnico):
Imagine $J(\theta)$ como uma superfície montanhosa em um espaço de alta dimensionalidade (cada dimensão é um parâmetro $\theta$). Você está em um ponto $\theta$ atual, envolto em neblina (sem visão global). O gradiente $\nabla J(\theta)$ é como uma bússola que mede a inclinação local mais íngreme para cima. Para descer, siga $-\nabla J(\theta)$. Em cada passo, recalcule o gradiente localmente — isso é o Gradiente Descendente Estocástico (SGD) ou variantes como Adam.

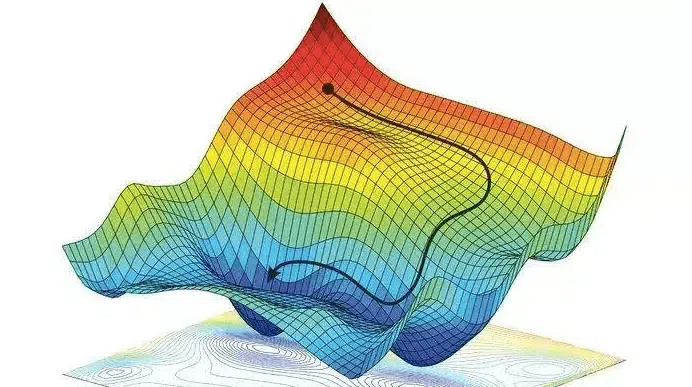
Em redes neurais, o gradiente é computado via backpropagation: propagamos o erro da saída para as camadas anteriores, usando a regra da cadeia para calcular derivadas parciais em cada peso.

Regra de Atualização dos Pesos

A atualização dos pesos segue o Gradiente Descendente:
$$ \theta_{\text{novo}} = \theta_{\text{antigo}} - \eta \cdot \nabla J(\theta) $$
onde $\eta$ (se pronuncia eta) é a taxa de aprendizado (learning rate), controlando o tamanho do passo.

• Escolha de $\eta$:
• Muito grande: Pode oscilar ou divergir (ex.: "pular" sobre o mínimo).
• Muito pequeno: Convergência lenta, risco de ficar preso em mínimos locais.
  Soluções comuns: Agendadores de learning rate (ex.: decaimento exponencial) ou otimizadores adaptativos como Adam, que ajustam $\eta$ por parâmetro com base em momentos de gradientes passados.

Em prática, para estabilidade, usamos mini-batches (SGD) em vez de batches completos, introduzindo ruído que ajuda a escapar de mínimos locais. Variantes avançadas incluem momentum (acelera em direções consistentes) e RMSProp (normaliza gradientes em dimensões variáveis).

O algoritmo passo a passo

1. Propagação direta (forward pass):

   • Os dados de entrada percorrem a rede camada por camada, gerando a saída final.

2. Cálculo do erro:

   • Comparação entre a saída prevista e a saída real usando uma função de custo (ex.: erro quadrático médio).

   Input → Camada1 → Camada2 → ... → Output → Calcular_Erro
   

   3. Propagação reversa (backward pass):
   • O erro é propagado de volta pela rede, calculando o gradiente de cada peso em relação ao erro.

3. Atualização dos pesos:

   • Cada peso é ajustado na direção que reduz o erro, de acordo com a taxa de aprendizado.

   Ajustar_Pesos ← ... ← Camada2 ← Camada1 ← Calcular_Gradientes ← Erro
   

Exercício Interativo – Passo a passo do Backpropagation

Neste exercício, você pode controlar a execução do backpropagation e visualizar:

• Como as ativações são calculadas na propagação direta.
• Como o erro se espalha de volta na propagação reversa.
• Como cada peso é atualizado após cada passo.

Controles disponíveis:

• Taxa de aprendizado (learning rate): Ajuste para ver como afeta a convergência.
• Função de ativação: Escolha entre Sigmoid, Tanh e ReLU.
• Botão "Próximo passo": Avança o backpropagation de forma manual.
• Botão "Treinar automático": Executa várias iterações seguidas.
• Mostrar gradientes: Ativa setas e valores numéricos sobre cada peso.

Objetivo:

Familiarizar-se com o funcionamento interno do backpropagation e entender o impacto da taxa de aprendizado e da função de ativação no treinamento.

Backpropagation – Passo a Passo

Taxa de aprendizado (η): 0.10

Função de ativação

Sigmoid Tanh ReLU

Próximo passo Treinar automático Reset

Época: 0

Erro (MSE): —

Saída prevista: —

Alvo (y): 1

Erro absoluto |ŷ − y|: —

Gradientes:

—

Curva de perda (MSE)

Para uma rede 2–2–1 com saída Sigmoid e MSE: $$ L=\tfrac12(y - \hat y)^2 \hat y=\sigma(z_2) z_2 = v_1 a_1 + v_2 a_2 + c a_i = g(z_i), z_i = w_{i1}x_1 + w_{i2}x_2 + b_i $$

As equações a seguir mostram como o erro é propagado da camada de saída para as camadas anteriores:

$$\begin{align} \frac{\partial \ell}{\partial z_2} &= (\hat{y} - y) \cdot \sigma'(z_2) \ \frac{\partial \ell}{\partial v_i} &= a_i \cdot \frac{\partial \ell}{\partial z_2} \ \frac{\partial \ell}{\partial a_i} &= v_i \cdot \frac{\partial \ell}{\partial z_2} \ \frac{\partial \ell}{\partial z_i} &= \frac{\partial \ell}{\partial a_i} \cdot g'(z_i) \ \frac{\partial \ell}{\partial w_{ij}} &= x_j \cdot \frac{\partial \ell}{\partial z_i} \end{align}$$

Essas equações formam a base do algoritmo de backpropagation, permitindo que os gradientes sejam calculados camada por camada, da saída para a entrada, para atualizar os pesos da rede neural de forma eficiente.

Reflexão:

1. O que acontece quando a taxa de aprendizado é muito alta? E quando é muito baixa?

2. Compare o comportamento do gradiente com Sigmoid, Tanh e ReLU.

3. Em qual caso o gradiente tende a "desaparecer" (vanishing gradient)?

4. Em qual caso o gradiente é mais estável?

5. Como o número de passos influencia na convergência do erro?

6. Observe o gráfico de erro:

7. Ele desce de forma suave ou com oscilações?

8. Há momentos em que o treinamento "trava"?

Por que o backpropagation calcula gradientes "de trás para frente"?

Porque é mais rápido computacionalmente

Porque usa menos memória

Porque o erro na saída é conhecido, facilitando o cálculo dos gradientes das camadas anteriores

Porque as camadas ocultas são mais importantes

Submit

Começamos pela saída porque conhecemos o erro desejado ali. Isso permite calcular como cada camada anterior contribuiu para esse erro, propagando a informação de volta pela rede.

Pseudocódigo

# Algoritmo Backpropagation Simplificado

def treinar_rede(rede, dados_treino, taxa_aprendizado):
    for cada_época:
        for cada_exemplo in dados_treino:

            # FORWARD PASS (predição)
            entrada = exemplo.dados
            for camada in rede:
                entrada = camada.processar(entrada)
            saída_predita = entrada

            # CALCULAR ERRO
            erro = exemplo.resposta_correta - saída_predita

            # BACKWARD PASS
            gradiente = calcular_gradiente_saída(erro)
            for camada in reversed(rede):
                gradiente = camada.calcular_gradiente(gradiente)
                camada.atualizar_pesos(gradiente, taxa_aprendizado)

Regra da cadeia

O backpropagation usa a regra da cadeia do cálculo para "quebrar" gradientes complexos em pedaços menores.

Funções de ativação e derivadas

Por que ReLU é tão popular? Sua derivada é super simples:

ReLU(x) = max(0, x)
Derivada = { 1 se x > 0
           { 0 se x ≤ 0

Sigmoid tem derivada mais complicada, tornando o cálculo mais lento.

Loss em classificação binária

• Didático (ok para este exercício): MSE com saída Sigmoid.
• Prática comum: Entropia Cruzada Binária (BCE) com saída Sigmoid — converge mais rápido e com gradientes mais estáveis.

Por que a derivada da função de ativação é importante no backpropagation?

Para determinar o número de neurônios necessários

Para escolher a arquitetura da rede

Para calcular como o erro se propaga através de cada neurônio

Para definir a taxa de aprendizado ideal

Submit

A derivada da função de ativação é essencial para aplicar a regra da cadeia e calcular como pequenas mudanças nos pesos afetam o erro final da rede.

Problemas comuns e soluções

1. Vanishing Gradients (gradientes que somem)

Problema: Em redes neurais com muitas camadas, o gradiente (que é a informação sobre o quão rápido a rede está aprendendo) se torna extremamente pequeno à medida que volta para as primeiras camadas. Isso faz com que os pesos nessas camadas iniciais sejam atualizados de forma muito lenta, impedindo a rede de aprender de maneira eficaz. É como se a informação de erro se "evaporasse" antes de chegar onde é mais necessária.

Soluções:

• Funções de Ativação: Troque funções como a Sigmoid ou tanh por ReLU (Rectified Linear Unit), que não "sufoca" o gradiente.
• Inicialização de Pesos: Comece o treinamento com pesos que não sejam nem muito grandes, nem muito pequenos. Técnicas como a inicialização de He ou de Xavier ajudam a manter os gradientes saudáveis.
• Normalização de Batch (Batch Normalization): Essa técnica ajusta as ativações dentro da rede, garantindo que os dados que fluem entre as camadas mantenham uma distribuição estável.
• Conexões de Salto (Skip Connections): Em arquiteturas como a ResNet, as camadas "pulam" e se conectam diretamente a camadas posteriores, criando um "caminho alternativo" para que o gradiente flua sem ser enfraquecido.

2. Exploding Gradients (gradientes que explodem)

Problema: É o oposto do anterior. O gradiente se torna extremamente grande, levando a atualizações massivas e instáveis nos pesos. Isso faz com que o modelo "exploda", e o treinamento não converge.

Soluções:

• Corte de Gradiente (Gradient Clipping): Simplesmente "corte" o gradiente quando ele atingir um valor muito alto, limitando-o a um limite pré-definido.
• Taxa de Aprendizado (Learning Rate) Menor: Reduza a taxa de aprendizado para que as atualizações de peso sejam mais graduais e menos propensas a "explodir".
• Inicialização Melhor: A mesma solução para o problema de "vanishing gradients" também ajuda a prevenir as explosões.

3. Overfitting

Problema: O modelo aprende os dados de treinamento com perfeição, mas não consegue generalizar para novos dados. É como um aluno que memoriza as respostas da prova, mas não entende a matéria. O modelo se torna bom demais nos dados que já viu, mas falha em aplicar o conhecimento em situações novas.

Soluções:

• Aumente os Dados: A maneira mais eficaz de evitar o overfitting é dar mais exemplos de treinamento para o modelo.
• Dropout: Durante o treinamento, essa técnica "desliga" aleatoriamente alguns neurônios em cada iteração. Isso força a rede a não depender de neurônios específicos, tornando-a mais robusta.
• Regularização (L1/L2): Adicione uma "penalidade" à função de perda para desincentivar pesos muito grandes. Isso ajuda a manter o modelo mais simples e com maior poder de generalização.
• Parada Antecipada (Early Stopping): Monitore a performance do modelo em um conjunto de validação e pare o treinamento assim que a performance começar a piorar.

O que caracteriza o problema de "vanishing gradients"?

A rede aprende muito rapidamente

Os pesos ficam muito grandes

Os gradientes se tornam muito pequenos nas camadas iniciais de redes profundas

A função de custo aumenta durante o treinamento

Submit

Vanishing gradients ocorre quando gradientes se tornam exponencialmente menores à medida que se propagam para trás, fazendo com que as primeiras camadas aprendam muito lentamente ou parem de aprender.

Otimizadores

SGD (Stochastic Gradient Descent): O básico

peso = peso - taxa_aprendizado × gradiente

Momentum: Adiciona "inércia"

velocidade = momentum × velocidade_anterior + gradiente
peso = peso - taxa_aprendizado × velocidade

Adam: Adapta taxa de aprendizado automaticamente

• Muito popular atualmente
• Combina momentum com adaptação automática

Learning Rate Scheduling

• Step decay: Reduz taxa periodicamente
• Exponential decay: Reduz exponencialmente
• Cosine annealing: Varia como coseno

Qual é a ideia central do algoritmo backpropagation?

Treinar apenas a última camada da rede

Usar apenas exemplos positivos para treinar

Propagar o erro da saída de volta através da rede para ajustar todos os pesos

Treinar cada camada separadamente

Submit

Backpropagation propaga o erro calculado na saída de volta através de todas as camadas, permitindo que cada peso seja ajustado proporcionalmente à sua contribuição para o erro final.

Por que a taxa de aprendizado é um hiperparâmetro crítico?

Porque determina o número de camadas da rede

Porque escolhe a função de ativação

Porque controla o tamanho dos ajustes nos pesos durante o treinamento

Porque define quantos dados usar para treinar

Submit

A taxa de aprendizado determina quão grandes são os passos de otimização. Muito alta pode causar instabilidade, muito baixa torna o aprendizado lento demais.

O que diferencia o backpropagation do aprendizado do Perceptron simples?

Backpropagation é mais lento

Backpropagation usa menos memória

Backpropagation pode treinar redes com múltiplas camadas ocultas

Backpropagation funciona apenas com ReLU

Submit

Enquanto o Perceptron só consegue ajustar pesos de uma única camada, backpropagation resolve o problema de como treinar todas as camadas de uma rede neural profunda simultaneamente.