Selection Sort

O Selection Sort é uma melhoria do Bubblesort, é um algoritmo de ordenação simples que divide a lista de entrada em duas partes: a sublista de itens já ordenados, que é construída da esquerda para a direita na frente (ou no topo) da lista, e a sublista de itens restantes a serem ordenados que ocupam o resto da lista. Inicialmente, a sublista ordenada está vazia e a sublista não ordenada é a lista inteira.

Funcionamento do Algoritmo

O algoritmo funciona repetidamente encontrando o menor (ou maior, dependendo da ordem de ordenação) elemento na sublista não ordenada, trocando-o com o elemento não ordenado mais à esquerda (ou seja, colocando-o na posição correta na sublista ordenada) e movendo a fronteira da sublista ordenada um elemento para a direita.

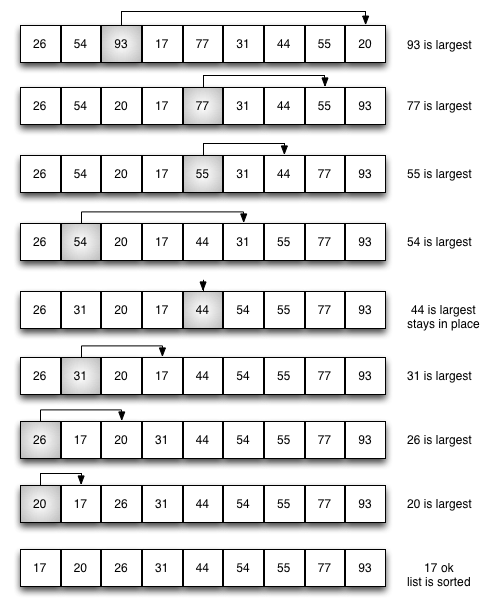
Selection Sort em ação

Para visualizar o algoritmo em ação utilize o link a seguir:

ttps://visualgo.net/en/sorting

Implementação em Python

Aqui está uma implementação simples do Selection Sort em Python:

def selection_sort(lista):
    n = len(lista)
    # Percorre a lista.
    for i in range(n):
        # Encontra o elemento mínimo da lista.
        minimo = i
        for j in range(i + 1, n):
            if lista[minimo] > lista[j]:
                minimo = j
        # Coloca o elemento mínimo na posição correta.
        lista[i], lista[minimo] = lista[minimo], lista[i] ## troca de posição

Uma variação possivel é modificar o algoritmo para ordenar colocando os maiores elementos no final, você precisaria procurar o maior elemento na sublista não ordenada em vez do menor. Isso pode ser feito alterando a condição de comparação no loop interno para if lista[idx] < lista[j]:. No entanto, na prática, isso não muda a essência do algoritmo; apenas inverte a ordem de ordenação.

def selection_sort(lista):
    n = len(lista)
    # Percorre a lista.
    for i in range(n):
        # Encontra o elemento máximo da lista.
        maximo = i
        for j in range(i + 1, n):
            if lista[maximo] < lista[j]:
                maximo = j
        # Coloca o elemento máximo na posição correta.
        lista[i], lista[maximo] = lista[maximo], lista[i]
    return lista

Neste caso, como exemplo:

lista = [64, 25, 12, 22, 11]
lista_ordenada = selection_sort(lista)
print("Lista Ordenada:", lista_ordenada)

Intuição da Análise de Complexidade

• Complexidade de Tempo: O Selection Sort tem uma complexidade de tempo quadrática O(n²), onde n é o número de elementos na lista. Isso ocorre porque ele precisa fazer duas passagens aninhadas sobre a lista para garantir que ela esteja ordenada.

• Complexidade de Espaço: A complexidade de espaço é O(1), pois requer apenas uma quantidade constante de espaço de memória adicional além da lista de entrada.

Exercício de Ordenação

Suponha que você tenha a seguinte lista de números para ordenar: [11, 7, 12, 14, 19, 1, 6, 18, 8, 20] qual lista representa a lista parcialmente ordenada depois de três passagens completas da ordenação por seleção,assumindo que vai buscar o maior elemento na sublista não ordenada em vez do menor?

• [7, 11, 12, 1, 6, 14, 8, 18, 19, 20]
• [7, 11, 12, 14, 19, 1, 6, 18, 8, 20]
• [11, 7, 12, 14, 1, 6, 8, 18, 19, 20]
• [11, 7, 12, 14, 8, 1, 6, 18, 19, 20]

Answer

A lista parcialmente ordenada depois de três passagens buscando o maior elemento na sublista não ordenada em vez do menor. [11, 7, 12, 14, 8, 1, 6, 18, 19, 20].

Referência: https://panda.ime.usp.br/panda/static/pythonds_pt/05-OrdenacaoBusca/AOrdenacaoPorSelecao.html