Merge Sort
Merge Sort¶
Agora que já entendemos um pouco sobre recursão, podemos avançar nossos estudos em algoritmos de ordenação mais complexos. O Merge Sort é um algoritmo de ordenação baseado na técnica de divisão e conquista.
Ele divide o conjunto de dados em metades menores, ordena essas metades e, em seguida, mescla as metades ordenadas para formar um conjunto ordenado. É conhecido por sua eficiência e estabilidade, sendo uma boa escolha para grandes conjuntos de dados. A complexidade de tempo do Merge Sort é O(n log n), onde n é o número de elementos na lista.
Funcionamento do Algoritmo¶
Divisão: Divide a lista em duas metades aproximadamente iguais.Conquista: Ordena recursivamente as duas metades.Combinação: Mescla as duas metades ordenadas para formar uma única lista ordenada.

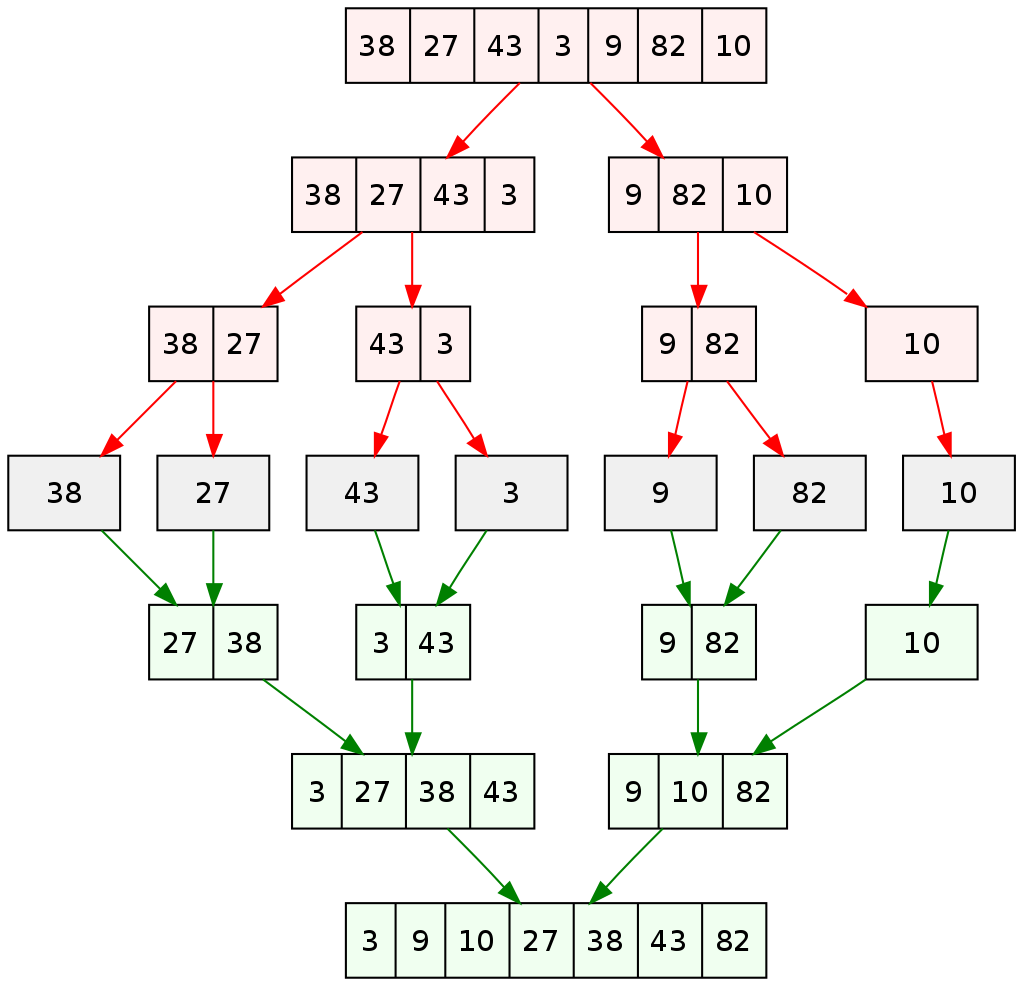
Merge Sort em ação¶
Para visualizar o algoritmo em ação, utilize o link a seguir:
https://visualgo.net/en/sorting?slide=7
Implementação em Python¶
Aqui está uma implementação simples do Merge Sort em Python:
def mergeSort(alist):
mergesort(alist, [0] * len(alist), 0, len(alist) - 1)
def merge(A, aux, esquerda, meio, direita):
"""
Combina dois vetores ordenados em um único vetor (também ordenado).
"""
for k in range(esquerda, direita + 1):
aux[k] = A[k]
i = esquerda
j = meio + 1
for k in range(esquerda, direita + 1):
if i > meio:
A[k] = aux[j]
j += 1
elif j > direita:
A[k] = aux[i]
i += 1
elif aux[j] < aux[i]:
A[k] = aux[j]
j += 1
else:
A[k] = aux[i]
i += 1
def mergesort(A, aux, esquerda, direita):
if direita <= esquerda:
return
meio = (esquerda + direita) // 2
# Ordena a primeira metade do arranjo.
mergesort(A, aux, esquerda, meio)
# Ordena a segunda metade do arranjo.
mergesort(A, aux, meio + 1, direita)
# Combina as duas metades ordenadas anteriormente.
merge(A, aux, esquerda, meio, direita)
Neste caso, como exemplo:
# Testa o algoritmo.
lista = [13, 30, 17, -1, -2, 27, 3]
mergeSort(lista)
print("Lista ordenada:", lista)
Intuição da Análise de Complexidade¶
-
Complexidade de Tempo: O Merge Sort tem uma complexidade de tempo O(n log n), que é mais eficiente que o Bubble Sort, especialmente para listas grandes.
-
Complexidade de Espaço: A complexidade de espaço é O(n), pois requer espaço adicional para armazenar as sublistas temporárias durante a ordenação.
Exercício de Ordenação
Suponha que você tenha a seguinte lista de números para ordenar: [29, 10, 14, 37, 13]. Qual lista representa a lista parcialmente ordenada depois da primeira divisão e conquista do merge sort?
- [29, 10, 14, 37, 13]
- [10, 29, 14, 13, 37]
- [14, 29, 10, 13, 37]
- [29, 14, 10, 37, 13]
Answer
A lista parcialmente ordenada depois da primeira divisão e conquista do merge sort é B. [10, 29, 14, 13, 37].
Exercise
Rode o código merge-sort utilizando o python tutor. (https://pythontutor.com/)[https://pythontutor.com/]. Execute o código passo a passo compare a complexidade de espaço de memória com o bubble-sort. Ele ocupa mais ou menos espaço de memoria?
Exercise
Escreva uma função recursiva baseada no método do merge-sort que ordene de forma decrescente um vetor aleatório de 15 posições.
https://algoritmosempython.com.br/cursos/algoritmos-python/pesquisa-ordenacao/mergesort/